I have become interested in formal methods lately. In particular, I have been learning Alloy recently. I came across a TLA+ model here, written by Leslie Lamport, who invented TLA+.

Here is the problem statement copied from the TLA+ code:

A farmer has a 40 pound stone and a balance scale. How can he break the stone into 4 pieces so that, using those pieces and the balance scale, he can weigh out any integral number of pounds of corn from 1 pound through 40 pounds.

Leslie Lamport named it a car talk puzzle. I thought it would be fun to try to solve this with Alloy. To define an Alloy model, we start with defining some signatures that introduces some structural concepts, followed by some constraints to reduce the search space. We can then ask the Alloy tool to execute some commands to find an instance or check an assertion.

For this puzzle, we will introduce 3 signatures. A signature is like a class in object-oriented programming.

The signature Piece represents a broken piece of the stone.

sig Piece {
  weight: Int -- The weight of the piece of stone
} {
  weight > 0
}

The weight field introduces a relation between Piece and Int, which represents the weight of the stone piece.

The signature Break represents a scenario of breaking the stone into several pieces. The field totalWeight is the weight of the stone. The field pieces is a sequence of the stone pieces. A sequence is like an array, whose elements can be accessed via indices into the array.

sig Break {
  totalWeight: Int, -- The weight of the stone
  pieces: seq Piece, -- The pieces that the stone is broken into
} {
  totalWeight > #pieces
  Piece in univ.pieces
  #pieces.elems = #pieces
  all i,j: pieces.inds | i < j => pieces[i].weight <= pieces[j].weight
  (sum i: pieces.inds | pieces[i].weight) = totalWeight
}

The signature facts, defined inside the second curly brace, specify some constraints. A fact is an assumption that always holds.

• The total weight of the stone is greater than the number of stone pieces,
• All Piece atoms belong to the pieces of a Break,
• Each Piece of a Break is unique,
• The pieces are sorted by the weight of the pieces,
• The total weight of the pieces is the same as the weight of the stone.

The signature Attempt represents an attempt of weighing the corn with stone pieces.

sig Attempt {
  left: set Int, // stone pieces put on the left side of the balance scale
  right: set Int // stone pieces put on the right side of the balance scale
} {
  no (left & right)
  #(left + right) > 0
  all i: (left + right) | i >= 0
}

The fields left and right contain the indices into the sequence of the stone pieces that will be put at the left or right side of the balance scale.

The signature facts state that

• A stone piece cannot be at both sides of the balance scale at the same time,
• There is at least one stone piece is put on the balance scale,
• The indices must be greater than 0.

With these signatures defined, we can define some constraints such that we can find a solution to the puzzle.

Let’s define a fact to ensure that each attempt is unique. We achieve this by specifying that, for every pair of distinct Attempts, their left fields or right fields should be different. The keyword disj indicates that the two attempts are disjoint.

fact "each_attempt_is_unique" {
  all disj t1, t2: Attempt |
    t1.left != t2.left or t1.right != t2.right
}

To make the code more readable and compact, we can define some functions. A function is introduced by the keyword fun.

The function SumWeight calculates that total weight of the selected ones from a sequence of stone pieces.

fun SumWeight[pieces: seq Piece, selected: set Int]: Int {
  sum i: selected | pieces[i].weight
}

The function AllValidBreaks returns all possible scenarios of breaking a Stone of weight w into n pieces.

fun AllValidBreaks[w: Int, n: Int]: set Break {
  { b: Break | #b.pieces = n and b.totalWeight = w }
}

The function AllWeights returns all weights that are greater than 0 and less than the given maxWeight.

fun AllWeights[maxWeight: Int]: set Int {
  { w: Int | w > 0 and w < maxWeight }
}

The function AllPossibleAttempts discovers all possible attempts. For each attempt, the number of the Integers of both left and right sides should not be more than the number of the stone pieces, the indices should be within the range, and the the total weight of the stone pieces at the left side should be less than that of the right side because the corn will be put at the left side.

fun AllPossibleAttempts[break: Break]: set Attempt {
  { t: Attempt | {
    #(t.left + t.right) <= #break.pieces 
    all i: (t.left + t.right) {
      i < #break.pieces
      SumWeight[break.pieces, t.left] < SumWeight[break.pieces, t.right]
    }
  }}
}

With all these functions, we can define some predicates. A predicate returns true or false when called.

The predicate CanMessure checks whether we can measure the corn, whose weight is w, by using the given stone pieces. It does this by checking if the total weight of the stone pieces put on the left side plus the weight of the corn equals to that of the stone pieces on the right side.

pred CanMeasure[w: Int, break: Break, attempt: Attempt] {
  w.plus[SumWeight[break.pieces, attempt.left]] = SumWeight[break.pieces, attempt.right]
}

The predicate IsSolution checks if a Break is a solution to the puzzle by checking if all the weights [1, maxWeight] can be measured with the given Break.

pred IsSolution[b: Break] {
  all w: AllWeights[b.totalWeight] | {
    some attempt: AllPossibleAttempts[b] | CanMeasure[w, b, attempt]
  }
}

Now we can ask the Alloy tool to find a solution for us. We define a command SomeSolution_40_4 and run it within the given scope. The command basically says “the 40 pound stone is to be broken into 4 pieces, find a Break that can weigh from 1 pound to 40 pound”. The for clause specifies a scope that has 4 atoms for each top level signature, but 7 Int and 40 atoms for Attempt. “7 Int” means the integers of 7 bits, which can represent any values in the range of [-64, 63].

run SomeSolution_40_4 {
  all b: Break | b.totalWeight = 40 and SumWeight[b.pieces, b.pieces.inds] = 40
  all t: Attempt | #(t.left + t.right) <= 4
  some b: AllValidBreaks[40, 4] | IsSolution[b]
} for 4 but 7 Int, 40 Attempt

After more than 6 minutes, the Alloy tool, running on my not-so-powerful laptop, gives a solution, which is to break the stone into 4 pieces whose weights are 1, 3, 9, and 27 pounds respectively.

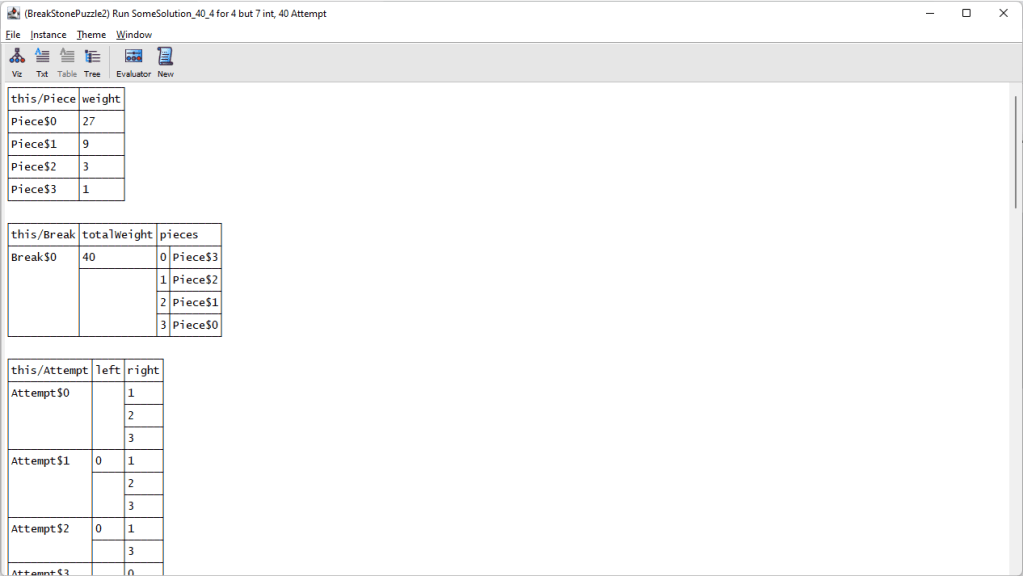
I write the code in such a way that it allows us to solve not only breaking a 40 pounds stone into 4 pieces, but also some other options, e.g. breaking a 13 pounds stone into 3 pieces. If we just want to solve breaking 40 pounds to 4 pieces, we can introduce more strict facts to reduce the search space, and thus reducing the time spent in finding a solution.

Alloy may not be a good tool for solving this kind of puzzles. However, it is very helpful when we want to examine the relationships among some structural concepts and specify a system precisely. Alloy 6 has introduced some new keywords to make it easier to specify dynamic behaviors.

I put the Alloy code here. You could paste the code into the editor of the Alloy tool and execute the commands.

module BreakStonePuzzle

/**
This is an attempt to converting a TLA+ model written by
Leslie Lamport to Alloy. The original TLA+ model can be found here:
	https://github.com/tlaplus/Examples/blob/master/specifications/CarTalkPuzzle/CarTalkPuzzle.tla

The following problem statement is copied from the TLA+ code.

(* Here is the problem.  A farmer has a 40 pound stone and a balance       *)
(* scale.  How can he break the stone into 4 pieces so that, using those   *)
(* pieces and the balance scale, he can weigh out any integral number of   *)
(* pounds of corn from 1 pound through 40 pounds.        

*/

-- A broken piece of the stone
sig Piece {
  weight: Int -- The weight of the piece of stone
} {
  weight > 0
}

-- Represent a break of the stone
sig Break {
  totalWeight: Int,	-- The weight of the stone
  pieces: seq Piece,	-- The pieces that the stone is broken into
} {
  -- The weight of the stone should be greater than the number of pieces
  totalWeight > #pieces

  -- Every piece is one of pieces of a break
  Piece in univ.pieces

  -- Each piece is unique
  #pieces.elems = #pieces

  -- The sequence of the pieces is sorted by the weight of the pieces
  all i,j: pieces.inds | i < j => pieces[i].weight <= pieces[j].weight

  -- The total weight of the pieces is the same as the weight of the stone
  (sum i: pieces.inds | pieces[i].weight) = totalWeight
}

-- An attemp to measure corn of certain weight
sig Attempt {
  left: set Int,  -- stone pieces put on the left side of the balance scale
  right: set Int  -- stone pieces put on the right side of the balance scale
} {
  -- A stone piece cannot appear at both sides of the balance scale
  no (left & right)

  -- There should be at least 1 stone piece 
  #(left + right) > 0

  -- The indices of all stone pieces should be non-negative
  all i: (left + right) | i >= 0
}

fact "each_attempt_is_unique" {
  all disj t1, t2: Attempt |
    t1.left != t2.left or t1.right != t2.right
}

-- Get the total weight of the selected stone pieces
fun SumWeight[pieces: seq Piece, selected: set Int]: Int {
  sum i: selected | pieces[i].weight
}

-- Get all valid breaks based on the given stone weight and the number of stone pieces
fun AllValidBreaks[w: Int, n: Int]: set Break {
  { b: Break | #b.pieces = n and b.totalWeight = w }
}

-- Get a set of weights based on the given maximal weight
fun AllWeights[maxWeight: Int]: set Int {
  { w: Int | w > 0 and w < maxWeight }
}

-- Check if the given weight can be measured with a break
pred CanMeasure[w: Int, break: Break] {
	-- The weight of the item plus the total weight of the stone pieces put
	-- at the left side of the balance scale should be equal to the 
	-- total weight of the stone pieces at the right side

	some attempt: Attempt {
		#(attempt.left + attempt.right) <= #break.pieces

		all i: attempt.left + attempt.right | i < #break.pieces

	  w.plus[SumWeight[break.pieces, attempt.left]] = SumWeight[break.pieces, attempt.right]
	}
}

-- Check if a break is a solution
pred IsSolution[b: Break] {
  all w: AllWeights[b.totalWeight] | {
    some attempt: AllPossibleAttempts[b] | CanMeasure[w, b, attempt]
  }
}

run SomeSolution_13_3 {
  some b: AllValidBreaks[13, 3] | IsSolution[b]
} for 4 but 5 Int, 13 Attempt

run SomeSolution_40_4 {
  some b: AllValidBreaks[40, 4] | IsSolution[b]
} for 4 but 7 Int, 40 Attempt